Flash AS绘制曲线的详细步骤

• Flash
• AS绘制曲线
• 详细步骤

曲线的绘制原理有两种：一种是由无数多或有限多的，即：lineTo绘制的曲线。

另一种是由函数计算并由曲线函数curveTo计算而成的。

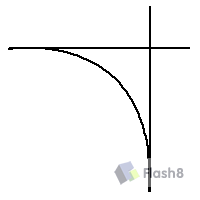
重点之重是讲第二点，最简单的曲线绘制代码：

this.lineStyle(1); 

this.moveTo(50,50); 

this.curveTo(100,100,200,100);

将上面的这三行代码直接放入一个空的flash里面,生成就可以看到一段曲线,这是怎么作出来的呢？

但是我们平时用到的如画出美丽的曲线很多都是对称并且是很平滑的,这个as能办到么? 答案是能。现在我们晋级来专注以下几个问题:曲线、对称、平滑。

曲线:

上面已经讲的很清楚了,但是为什么还要讲呢?主要是用as来控制曲线一定要以曲线的原理来为曲线分段,从而得到相应的节点。如上图,你看到的曲线和下图被分割的一样么,也许用钢笔[绘画软件里面的工具]绘制是同一条线,但是用as来绘制的话就是这样的。上面的曲线是两个点组成的一条曲线,下面的是由三个点组成的两条曲线,分清这些才能继续深入研究as曲线的构造[不过也有例外,即使平滑的单条曲线也可由多条曲线线段组成,不过这样做没有太大意义]。***[以曲线的两个点作射线可交在一起,此点为flash函数中控制曲线的点的位置]***

平滑:

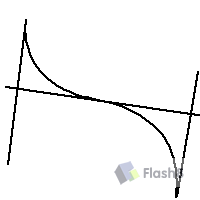
什么是平滑呢?在曲线与曲线之间过渡不僵硬就代表平滑了,比如圆、椭圆等,平滑能够使效果看上去很舒服。最平滑的方法是这样的,最简单的3点ABC,当AB的曲线固定位置后c曲线可任意 但是c曲线因为平滑会受到某些限制，即前面曲线的控制点要和B点以及BC所绘制的曲线的控制点要在一条直线上,如下图：

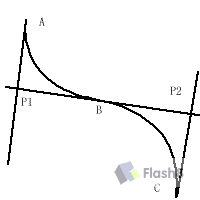
p2可以在p1和B的延长线上移动,但是不能移动到B左侧,否则曲线无法平滑。

对称:

例如一个圆,要做到用as来绘制,是十分难的,最上面提到的最简单的代码,如果你用手动尝试来一次次试验,犹如像爱迪生一样屡屡失败,无法达到预期的效果，在这个问题之前应该看一下例图：

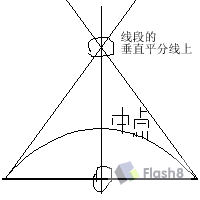
我们会发现曲线为对称时,曲线的控制点也在两端点连线的垂直平分线上,那么我们就来讨论如何得到以中点垂直直线所得到的线上的任意点吧！ 

垂直平分线上的任意点:

对于几何,大家可以很简单的得到这个问题的答案 但是大家想想看,如果对于任意角度的线段由as来得到显然有点难度。毕竟是编程,没有什么难不倒大家的,我们找找材料吧。发现了!flash8里面内置了一个类point,其实这个类很简单,如果大家只是为了冲着point类而生成flash8的文件,那就太浪费了,因为这个类完全可以自己写，我在最下面把它整理上来,帮助大家使用[这个类我结合了vect2d和point两个方法总结到一起,大家别嫌代码多啊 呵呵]。中点那个方法是point.verticalPoint(点1,点2,与中点的距离[可以为正/负])。这个函数的原理我不知道是不是最方便的。在此把思路告诉大家,取任意两点AB,得到其中点O,将AB点分别复制为A’B’点并让此克隆点[clone方法],以原来的点旋转[即A’相对B旋转,B’相对A点旋转],得出此新的两点,进一步又得到两个新点的中点O’,如图：

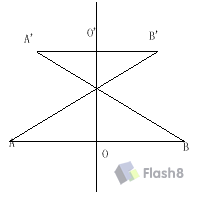
再在OO’上取相对O定长的点很容易。再回到刚才的问题上来就很容易解决对称曲线的问题了。曲线真是一种很奇妙的东西，com_zszen是我的自定义类包[pakage适合flash7以上版本]，里面包括了一个math类和一个point类,你可以通过研究我的代码来达到学习的目的。

还有就是我上面忘了提到一点:

关于闭合以及非闭合平滑过渡曲线的绘制,显然你通过找点是无法实现的,或是说你无从下手,也就是说给你两个以上的点,他们的曲线控制点是任意的,也就是说你第一个点决定了你的去曲线的行走方式.所以这样显然不能得到我们想要的曲线。所以我认为应该从曲线的控制点考虑,也就是说曲线的控制点如果都已知,那么就ok了。

我的方法是建立一个方程 以p1=curveX(target,p1,p2,p3),将追踪得到新的控制点,当然第一次运行不会绘制上来,也就是说运行此程序还存在效率问题,就是n个点的闭合曲线要运行n+1次,n个点的非闭合曲线要运行n次,而非闭合的起始点就成为了无法绘出的曲线位置,我的这个程序对于精确的曲线运算,没有足够的重视,如果说实现一些效果,应当是可以的,[其中用过联想广告的噪音声波图]。     

static function curvePlus(path:MovieClip, a1, control1, control2, doNoDraw:Boolean) { 

path.moveTo(a1.x, a1.y); 

var c1 = new point(control1.x, control1.y); 

var c2 = new point(control2.x, control2.y); 

var m = point.interpolate(c1, c2, 0.5); 

if (doNoDraw == true) { 

return (m); 

} 

path.curveTo(c1.x, c1.y, m.x, m.y); 

//curveTo(c2.x, c2.y, a2.x, a2.y);   

return (m); 

}